Mighty Mouse
WKR
I don't think FOC has any effect on the angle an arrow adopts during flight. I do think that a slower arrow will fly more tip down and that the effect of reduced speed on flight angle gets mistakenly attributed to increased FOC. When guys dabble with high FOC, they often don't hold total arrow weight (and thus speed) constant, they just add a bunch of weight to the front and see what happens. The results then get ascribed to increased FOC when they're often a product of increased total arrow weight (and/or reduced speed). I submit my thesis to the scrutiny of the 'slide:I've heard it, but haven't understood it. How does an arrow fly tip down just because it's EFoc? The drag of the fletching should be correcting that. It might do it for the first bit, but the fletching will pull the back of the shaft behind the point unless it doesn't have enough drag.
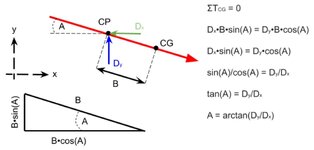
Disregarding possible near-launch aberrations due to the bow being out of tune, any arrow shot toward a horizontal target begins flying with the tip pointed above horizontal because the shooter intentionally (and necessarily) aims the bow/arrow at an angle above (typically just slightly above) horizontal. The arrow maintains a positive (tip up) angle until it reaches the apex of its trajectory. At the apex, the arrow's angle relative to horizontal momentarily becomes zero (parallel to the ground) then becomes negative (tip down) for the remainder of its flight. The negative angle post-apex is caused by drag force acting in the vertical direction. We typically only think about drag acting horizontally along the length of the arrow and working to slow the arrow's forward progress, but because the arrow is also traveling vertically as it travels horizontally toward the target, there is also a drag force acting vertically. Both drag forces (horizontal and vertical) act through the arrow's "center of pressure" (CP), the location of which is largely determined by amount of fletching and lies rearward of the midpoint on an adequately fletched arrow. After the arrow reaches the apex of its trajectory and begins falling, vertical drag (shown as Dy in the sketch below) is directed upward, which tries to rotate the arrow clockwise around its center of gravity (CG). This rotational force (aka, torque) is counteracted by the horizontal drag force (Dx) acting in the negative x direction (leftward in the sketch), which tries to rotate the arrow counterclockwise around its CG. The magnitudes of these torques can be quantified by multiplying the linear force values by the perpendicular distances between the arrow's CP and CG. These perpendicular distances (aka, lengths of the "moment arm") are equal to the distance (B) along the arrow shaft between CP and CG multiplied by the sine and cosine, respectively, of the arrow's angle (A) relative to horizontal. At any given instant, the drag-induced torques acting around the arrow's CG are equal and opposite; thus, Dx•B•sin(A) = Dy•B•cos(A). B appears on both sides of the equation and thus cancels out, meaning that the location of CG (and therefore the amount of FOC) has no effect on the angle relative to horizontal that the arrow adopts during flight. The calculation of A resolves to the inverse tangent of the ratio of drag forces, arctan(Dy/Dx), meaning drag forces alone determine angle A regardless of CG or CP location (or, by extension, amount of FOC). Drag forces are directly proportional to speed, so Dx would certainly be smaller for a slower arrow. I think Dy would remain relatively constant, or possibly increase due to longer flight time and thus more time for gravitional acceleration to take effect. If true, this would cause the ratio of drag forces (Dy/Dx) to increase and the magnitude of the angle relative to horizontal, calculated as arctan(Dy/Dx), to increase, meaning a slower arrow would tend to fly at a more negative (tip down) angle. At moderate ranges with fast bows, the angle differences are so slight that they're difficult to discern. At longer ranges as the arrow slows significantly, it's easier to see the tip down terminal angle.
Last edited:
