- Joined
- Feb 6, 2025
- Messages
- 24
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
What you refer to is the "Magnus Effect," which is a result of Bernoulli's equation for fluid flow applied to spinning bullets. Essentially, from conservation of energy, the energy in the air flowing around an object is partitioned into velocity and pressure. Increased flow speed means a reduction in pressure. Depending upon bullet spin direction and wind direction, pressure will be either increased or decreased above or below the spinning bullet in a cross wind, leading to a small rise or drop of the bullet. A bullet yawing will also induce a slight component of upward/downward Magnus force by creating a component of cross flow, even in still air. Here's a good picture on a great website that discusses many other aspects of both gyroscopic stability and dynamic stability of bullets (warning - this site suffers a bit from translation - some explanations of the physics are not exactly correct):View attachment 865391View attachment 865392
Fairly new to shooting but is there actually 4” of elevation change at 300 yards depending on cross wind direction? Shooting a 300 rum nosler accubond 200gr (.588 g1 bc) at 3100 fps.
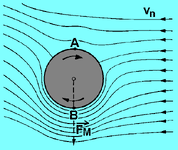
I disagree. This one got me too, I had to go through that same site and others to “get it”. My brain was stuck on the idea of “lift” like an airplane wing, similar to magnus effect.What you refer to is the "Magnus Effect," which is a result of Bernoulli's equation for fluid flow applied to spinning bullets. Essentially, from conservation of energy, the energy in the air flowing around an object is partitioned into velocity and pressure. Increased flow speed means a reduction in pressure. Depending upon bullet spin direction and wind direction, pressure will be either increased or decreased above or below the spinning bullet in a cross wind, leading to a small rise or drop of the bullet. A bullet yawing will also induce a slight component of upward/downward Magnus force by creating a component of cross flow, even in still air. Here's a good picture on a great website that discusses many other aspects of both gyroscopic stability and dynamic stability of bullets (warning - this site suffers a bit from translation - some explanations of the physics are not exactly correct):
View attachment 865439
Nois there actually 4” of elevation change at 300 yards depending on cross wind direction?
I appreciate your well-written response and this discussion, but I think you may be conflating "gyroscopic stability" with "dynamic stability." Gyroscopic stability, as you mentioned, is a measure of the bullet's ability to resist yawing and/or pitching due to the application of external moments. But dynamic stability measures the bullet's ability to reduce yawing over time. If perturbed, the bullet's yaw angle might increase with time as it yaws back and forth (unstable), reduce over time (stable), or not increase or decrease - it wags back and forth without change in yaw rate (marginally stable). Both phenomena are not directly dependent; a bullet can be dynamically stable but not gyroscopically stable, or vice versa, or unstable or stable by both measures. Your thoughts?I disagree. This one got me too, I had to go through that same site and others to “get it”. My brain was stuck on the idea of “lift” like an airplane wing, similar to magnus effect.
Aerodynamic “spin” jump and Aerodynamic “spin” drift occur because of the gyroscopic stability of a bullet creating what is called nutation and precession (think of the tip of the bullet spinning and making little tiny circles) as the bullet continually “self corrects” with the “balancing” effect of spin when any wind disrupts its flight.
Look at the way the body of the top in the video “wobbles” but nothing is touching but the tip. It is spin that moves the body of the top in space to keep it balanced.
It isn’t caused by the pressure difference described by the Magnus effect.
The spin of a bullet does the same thing as spin of a top. When wind and air resistance pushes/destabilizes a bullet, the gyroscopic spin moves/reorients/points the entire body of the bullet in space—just like the top.
It has to rebalance itself by “shifting its weight” back to balanced. Basically, the bullet is stable only because the spin is constantly correcting from deflections.
From the same website, here is the fancy way of saying the bullet moves perpendicular—up or down— to the wind force. It’s not caused by differences in air pressure cause by a spinning body.
“A spin-stabilized projectile is said to be gyroscopically stable, if, in the presence of a yaw angle d, it responds to an external wind force F1 with the general motion of nutation and precession. In this case the longitudinal axis of the bullet moves into a direction perpendicular to the direction of the wind force.”
I know what I know, and some things are even true…I appreciate your well-written response and this discussion, but I think you may be conflating "gyroscopic stability" with "dynamic stability." Gyroscopic stability, as you mentioned, is a measure of the bullet's ability to resist yawing and/or pitching due to the application of external moments. But dynamic stability measures the bullet's ability to reduce yawing over time. If perturbed, the bullet's yaw angle might increase with time as it yaws back and forth (unstable), reduce over time (stable), or not increase or decrease - it wags back and forth without change in yaw rate (marginally stable). Both phenomena are not directly dependent; a bullet can be dynamically stable but not gyroscopically stable, or vice versa, or unstable or stable by both measures. Your thoughts?
Sorry, I edited my post (again) likely before you posted your response. In effect, the Magnus force (a consequence of the Bernoulli Principle), generally acts to induce a twist, or moment (aka, the Magnus Moment), around the center of mass of the bullet (unless the line of action of the Magnus force so happens to intersect the center of mass, in that case, no twist at all). The only way to change the angular momentum of a body is to apply an external moment to the body. Vectorial addition provides the change in the original angular momentum vector of the body. Thus, my interpretation is that the Magnus force causes either upward or downward acceleration of the bullet, while the Magnus Moment causes a change in the magnitude and direction of the angular velocity vector of the bullet. Wind will cause an external distributed load on the bullet; this too will result in a moment vector applied to the bullet, causing yet another change in the angular velocity vector of the bullet. My 0.02 cents, anyway....Back to the magnus effect, did you cede that point? We are talking about wind deflection and jump.
Not sure whether you did with your switch to difference between two types of “stability”.
Correct me if I’m wrong but from how I understand it if the wind is coming from the right to left and the bullet spin is rolling the wind underneath the bullet causing it to rise? Left wind causes the bullet to roll the wind over the top due to the spin pushing it down? Is this kind of a dumbed down version?Wind destabillizes a bullet and the gyroscopic spin stabilizes the bullet. It spins like a top in little circles within circles. Spin a top with a right twist, if it is hit from the right side the stabilization starts on the left side of the circles and gyroscopic forces correct towards the disturbance to the right. You can see the top “lean into” the disturbance as it stabilizes spinning in the corkscrew sort of shapes. That is called precession.
With a right twist gyroscopic spin, the direction of travel is always the direction leaning into the disturbance to get balance, whether a top or a bullet.
If I push your right shoulder, you are forced right and muscles lean left to correct. A bullet is spinning, so it corrects its balance with the spinning gyroscope stability.
Gyroscopic stability has a vertical component because a circular correction has a vertical component in addition to the lateral correction. The vertical component is “aerodynamic jump”
Imagine corrections happening using clock positions.
A right wind pushes a bullet left to the 9:00 position. The bullets spin causes travel up and to the right towards 12:00 in the circles to get stabilized. That is the vertical change as a result of the wind, “jumping” up.
If you touch it on the left, the disturbance is corrected starting from the right side of the circle at 3:00. To gyroscopically “balance” itself, it continues the right hand twist/circle down to 6:00 and to the left. That is the vertical “jump” down.
So, a right wind moves a bullet “up”—actually it falls less compared to no wind because of the gyroscopic movement. And, a left wind moves a bullet down.
How much is the difference actually? You have to shoot it to know for sure and it will depend on everything that affect gyroscopic stability plus the time of flight.
Yes, but a 10mph wind at 300 yds still won't amount to anything like a 4"elevation change. There will be a tiny amount but hardly enough to even see or care about in a hunting situation. No idea why Hornady is showing that much of an error but it seems a common complaint when using the Hornady 4DOF and a non-Hornady bullet.Is this kind of a dumbed down version?
You, that image is something I picture too. I visualize the wind as a line that touches the bullet, and then think which way the bullet goes in relation to the line.Correct me if I’m wrong but from how I understand it if the wind is coming from the right to left and the bullet spin is rolling the wind underneath the bullet causing it to rise? Left wind causes the bullet to roll the wind over the top due to the spin pushing it down? Is this kind of a dumbed down version?
Yes, but a 10mph wind at 300 yds still won't amount to a 4"elevation change. There will be some but not enough to see or care about in a hunting situation. What you do care about is the total left right drift, not the minute elevation change. No idea why Hornady is showing that much of an error but it seems a common complaint when using the Hornady 4DOF and a non-Hornady bullet. Get yourself something simple like Shooter, turn off Coriolis and aero jump and carry on.Is this kind of a dumbed down version?
Yes, you've got to test some of these things out. It seems a lot to me, but then again, who knows...Yes, but a 10mph wind at 300 yds still won't amount to anything like a 4"elevation change. There will be a tiny amount but hardly enough to even see or care about in a hunting situation. No idea why Hornady is showing that much of an error but it seems a common complaint when using the Hornady 4DOF and a non-Hornady bullet.
Deep is the only way, my friend... hahahahahaDeep. LOL.
I knows you aren't even going to see 2" at 300 with a L R 10 mph wind swap even with a worse bullet. I've shot a lot of 165SMK's at much slower velocity than the OP's RUM and he's just not going to see it. BTDTYes, you've got to test some of these things out. It seems a lot to me, but then again, who knows...
I knows you aren't even going to see 2" at 300 with a L R 10 mph wind swap even with a worse bullet. I've shot a lot of 165SMK's at much slower velocity than the OP's RUM and he's just not going to see it. BTDT
