pyrotechnic
Lil-Rokslider
- Joined
- Nov 7, 2019
- Messages
- 249
I’m pretty new to this forum, I lurked for a while before I joined and the membership here has guided a lot of purchases regarding tents, sleeping bags, pads, clothing, and binoculars. Not to mention hours upon hours of entertainment reading threads on hunting and getting to live and learn vicariously through the experiences of the members of this board. I’ve seen a lot of similar posts asking questions regarding ballistic calculators and I’m hoping that this can bring some clarity and understanding to what can frustratingly look like magic to those just starting to use them. Or maybe I’ll just bring some more confusion.
I’m going to show a little bit of math and then try to break it down into layman’s terms so that the reader can get a better understanding how these apps work. I wrote a rudimentary program using MATLAB that managed to match Applied Ballistics solutions given the same inputs. Although my program was the mathematical equivalent of headbutting a door until it opened, the process was very insightful for me, and I hope that I can translate that experience into something useful for the membership here. I am going to assume that the reader knows what a Mil-radian and Minute of Angle is.
First what is a point mass solver? It is a program that treats the projectile as point in space that has mass and velocity, the forces on it (drag & gravity) are calculated and the program steps through time recalculating these drag forces at each step. 3 degrees of freedom (DOF) x, y, z are considered. These correspond to distance, drift, and drop and allow the program to determine the location of the "point" at a place in time. For higher degrees of freedom programs, the rotation about these axis’ are considered, up to 6DOF. The more degrees of freedom, the more information about the projectile you need to make an accurate model. My knowledge is limited to what makes a 3 DOF model and is not entirely comprehensive at that. In my experience, 3 DOF models are quite accurate within the supersonic portion of a projectile’s flight.
I’m not going to get into Coriolis, Spin Drift, Aerodynamic Jump etc. This is a big can of worms that gets people quite heated. My thoughts are below and I’m going to leave it at that. I haven’t seen any improvement by utilizing them in MY solutions for the shooting that I do. Coriolis is pretty simple to calculate and I would imagine most 3 DOF programs do a good job of it. I don’t believe 3DOF can give us anything other than a “guess” on spin drift and I turn it off. Aerodynamic jump is a small vertical deflection due to your spinning projectile hitting a crosswind as it exits the muzzle. I haven’t investigated it to say how well programs calculate it, but it is small, and for the way I use these programs I find it extremely irritating when I cannot “turn it off” like I can spin drift and Coriolis.
Inputs
Garbage in = Garbage out. Most errors are due to incorrect inputs. I’m going to try to explain inputs and why they do/don’t matter.
Muzzle Velocity: this is the speed of the projectile as it exits the barrel, drag forces immediately start slowing the bullet down so this is the fastest the bullet will ever go.
Ballistic Coefficient: This number essentially scales the acceleration of the bullet due to drag. It is a function of sectional density and form factor (sleekness if you will). Just as a high sectional density will penetrate a game animal better a high sectional density will “penetrate” the air better. Having a pointy bullet with a boat tail helps it do that even more. There are 2 different BC’s that are commonly used, the G1 and the G7. Make sure that if you are using a G1 BC if you are using the G1 drag function and vice versa.
Weight: Changing the bullet weight in the program will only change the kinetic energy numbers downrange. Changing the weight will not change the calculated trajectory if you don’t’ change the BC.
Zeroing range: The baseline from which the program will give you corrections. I usually zero at 100 yds, most rifle ranges will go out that far, and at that distance atmospherics have had a negligible effect on your zero. Example: a 100yd zero at sea level is a 100 yd zero at 10000 ft of altitude. If you zeroed at 300 yds at sea level you would not be zeroed at 300 yds at 10000ft.
Zero Height: If your point of impact is 2” high at your zeroing range this is where you would put that.
Zero Offset: Horizontal deviation of your POI from your POA. If you only shoot one round this can seem a rather dumb option to have, however if you shoot different ammo types or suppressed vs unsuppressed your program can account for this.
Sight Height: Since our scope sits above the bore and gravity starts pulling the bullet down as soon as it leaves the barrel, we have to launch the projectile upwards in relation to our line of sight in order for our light of sight and the trajectory of the bullet to intersect. The Sight Height and zeroing distance has an effect on the upward angle at which we launch the bullet. Small errors aren’t a big deal but try to get this number fairly close.
Sight Offset: this is the horizontal distance between our bore and our optic. Modern rifles don’t generally have this issue but this will allow the program to account for windage differences past the zeroing range if your optic isn’t mounted above your bore.
Twist rate: This is given in inches per complete rotation of the projectile as it travels down the bore, example a 1:10 twist barrel with spin the bullet one rotation for every 10 inches it goes down the barrel. Longer bullets require faster twists than short squat ones to keep them stabilized. The twist rate in your calculator will only effect things like spin drift and aerodynamic jump if the program is calculating them.
Elevation Correction Factor: This allows you to correct for a scope that is repeatable, but doesn’t track perfectly. The way you find out is by a tall target test. Example: on you test you dial 10 mils, but your point of impact moves 9.8 mills. Your correction factor would be 0.98. Unless you have tested is and know the “error” this number should be 1.0
Windage Correction Factor: Same as above but for windage.
Temperature: This affects the density of the air, the lower the temperature the denser the air. The speed of sound in an ideal gas (how we model air) is solely dependent on the temperature. The drag coefficient of the bullet is a function of its Mach number (the ratio of its speed to the speed of sound). This is also why using Density Altitude isn’t quite as accurate as a measured pressure and temperature
Pressure: This also affects the density of the air, the higher the pressure the denser the air.
Humidity: Again, this affects air density. Lower the humidity the denser the air, this seem counterintuitive, but it is the reason clouds don’t come crashing down into the ground. Humidity has a very low impact on air density so I usually just leave it at 50% and never touch it.
Density Altitude: This is a way to wrap pressure, temperature, and humidity into a nice single number of equivalent air density. Its super handy for quick reverence range cards if you’re in the mountains and elevation and temperature changes happen throughout your hunt. I will not be quite as accurate as utilizing a measured temperature and pressure, as the speed of sound in air is entirely dependent on temperature.
Look angle: This is the angle from you to the target. Relative to you line of sight, the projectile drop less if you are shooting up or down.
How are the Inputs used?
Below is the equation that calculates the acceleration of the bullet due to drag, and a plot of drag coefficients vs Mach number
v=velocity of the bullet, BC=Ballistic coefficient, ρ=Air density, and Cd(M)= the drag coefficient as a function of the Mach number M.
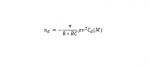

Starting off, v is our muzzle velocity. ρ was calculated using Temperature, Pressure, and Humidity. The Mach number (M) is calculated by the ratio of v to the speed of sound which was determined by our air temperature. This is where the G1 or G7 drag function come into play. The program used that Mach number to determine the corresponding Drag coefficients (Cd). The acceleration of that bullet due to drag is then calculated. Multiplying that acceleration by a period of time gives us the change in velocity over that time. The new velocity is then substituted for v and the cycle repeats, a new M is calculated, a new Cd is referenced and the equation is then again solved. Because modern computers can do these steps super quickly over and over, we can make this time step really small and approximate a continuous de-acceleration of the projectile. At the same time the constant gravitational acceleration is applied to get drop.
The only thing that affects the amount a projectile will drop is time of flight. If you are shooting downhill or uphill your line of sight is now no longer perpendicular to gravity and a component of your “drop” is now parallel to your line of sight. Wind drift is determined by the difference between time of flight in a vacuum and actual time of flight. This is why BC is king when it comes to wind drift, a high BC will shrink that difference.
I’m going to show a little bit of math and then try to break it down into layman’s terms so that the reader can get a better understanding how these apps work. I wrote a rudimentary program using MATLAB that managed to match Applied Ballistics solutions given the same inputs. Although my program was the mathematical equivalent of headbutting a door until it opened, the process was very insightful for me, and I hope that I can translate that experience into something useful for the membership here. I am going to assume that the reader knows what a Mil-radian and Minute of Angle is.
First what is a point mass solver? It is a program that treats the projectile as point in space that has mass and velocity, the forces on it (drag & gravity) are calculated and the program steps through time recalculating these drag forces at each step. 3 degrees of freedom (DOF) x, y, z are considered. These correspond to distance, drift, and drop and allow the program to determine the location of the "point" at a place in time. For higher degrees of freedom programs, the rotation about these axis’ are considered, up to 6DOF. The more degrees of freedom, the more information about the projectile you need to make an accurate model. My knowledge is limited to what makes a 3 DOF model and is not entirely comprehensive at that. In my experience, 3 DOF models are quite accurate within the supersonic portion of a projectile’s flight.
I’m not going to get into Coriolis, Spin Drift, Aerodynamic Jump etc. This is a big can of worms that gets people quite heated. My thoughts are below and I’m going to leave it at that. I haven’t seen any improvement by utilizing them in MY solutions for the shooting that I do. Coriolis is pretty simple to calculate and I would imagine most 3 DOF programs do a good job of it. I don’t believe 3DOF can give us anything other than a “guess” on spin drift and I turn it off. Aerodynamic jump is a small vertical deflection due to your spinning projectile hitting a crosswind as it exits the muzzle. I haven’t investigated it to say how well programs calculate it, but it is small, and for the way I use these programs I find it extremely irritating when I cannot “turn it off” like I can spin drift and Coriolis.
Inputs
Garbage in = Garbage out. Most errors are due to incorrect inputs. I’m going to try to explain inputs and why they do/don’t matter.
Muzzle Velocity: this is the speed of the projectile as it exits the barrel, drag forces immediately start slowing the bullet down so this is the fastest the bullet will ever go.
Ballistic Coefficient: This number essentially scales the acceleration of the bullet due to drag. It is a function of sectional density and form factor (sleekness if you will). Just as a high sectional density will penetrate a game animal better a high sectional density will “penetrate” the air better. Having a pointy bullet with a boat tail helps it do that even more. There are 2 different BC’s that are commonly used, the G1 and the G7. Make sure that if you are using a G1 BC if you are using the G1 drag function and vice versa.
Weight: Changing the bullet weight in the program will only change the kinetic energy numbers downrange. Changing the weight will not change the calculated trajectory if you don’t’ change the BC.
Zeroing range: The baseline from which the program will give you corrections. I usually zero at 100 yds, most rifle ranges will go out that far, and at that distance atmospherics have had a negligible effect on your zero. Example: a 100yd zero at sea level is a 100 yd zero at 10000 ft of altitude. If you zeroed at 300 yds at sea level you would not be zeroed at 300 yds at 10000ft.
Zero Height: If your point of impact is 2” high at your zeroing range this is where you would put that.
Zero Offset: Horizontal deviation of your POI from your POA. If you only shoot one round this can seem a rather dumb option to have, however if you shoot different ammo types or suppressed vs unsuppressed your program can account for this.
Sight Height: Since our scope sits above the bore and gravity starts pulling the bullet down as soon as it leaves the barrel, we have to launch the projectile upwards in relation to our line of sight in order for our light of sight and the trajectory of the bullet to intersect. The Sight Height and zeroing distance has an effect on the upward angle at which we launch the bullet. Small errors aren’t a big deal but try to get this number fairly close.
Sight Offset: this is the horizontal distance between our bore and our optic. Modern rifles don’t generally have this issue but this will allow the program to account for windage differences past the zeroing range if your optic isn’t mounted above your bore.
Twist rate: This is given in inches per complete rotation of the projectile as it travels down the bore, example a 1:10 twist barrel with spin the bullet one rotation for every 10 inches it goes down the barrel. Longer bullets require faster twists than short squat ones to keep them stabilized. The twist rate in your calculator will only effect things like spin drift and aerodynamic jump if the program is calculating them.
Elevation Correction Factor: This allows you to correct for a scope that is repeatable, but doesn’t track perfectly. The way you find out is by a tall target test. Example: on you test you dial 10 mils, but your point of impact moves 9.8 mills. Your correction factor would be 0.98. Unless you have tested is and know the “error” this number should be 1.0
Windage Correction Factor: Same as above but for windage.
Temperature: This affects the density of the air, the lower the temperature the denser the air. The speed of sound in an ideal gas (how we model air) is solely dependent on the temperature. The drag coefficient of the bullet is a function of its Mach number (the ratio of its speed to the speed of sound). This is also why using Density Altitude isn’t quite as accurate as a measured pressure and temperature
Pressure: This also affects the density of the air, the higher the pressure the denser the air.
Humidity: Again, this affects air density. Lower the humidity the denser the air, this seem counterintuitive, but it is the reason clouds don’t come crashing down into the ground. Humidity has a very low impact on air density so I usually just leave it at 50% and never touch it.
Density Altitude: This is a way to wrap pressure, temperature, and humidity into a nice single number of equivalent air density. Its super handy for quick reverence range cards if you’re in the mountains and elevation and temperature changes happen throughout your hunt. I will not be quite as accurate as utilizing a measured temperature and pressure, as the speed of sound in air is entirely dependent on temperature.
Look angle: This is the angle from you to the target. Relative to you line of sight, the projectile drop less if you are shooting up or down.
How are the Inputs used?
Below is the equation that calculates the acceleration of the bullet due to drag, and a plot of drag coefficients vs Mach number
v=velocity of the bullet, BC=Ballistic coefficient, ρ=Air density, and Cd(M)= the drag coefficient as a function of the Mach number M.
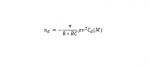

Starting off, v is our muzzle velocity. ρ was calculated using Temperature, Pressure, and Humidity. The Mach number (M) is calculated by the ratio of v to the speed of sound which was determined by our air temperature. This is where the G1 or G7 drag function come into play. The program used that Mach number to determine the corresponding Drag coefficients (Cd). The acceleration of that bullet due to drag is then calculated. Multiplying that acceleration by a period of time gives us the change in velocity over that time. The new velocity is then substituted for v and the cycle repeats, a new M is calculated, a new Cd is referenced and the equation is then again solved. Because modern computers can do these steps super quickly over and over, we can make this time step really small and approximate a continuous de-acceleration of the projectile. At the same time the constant gravitational acceleration is applied to get drop.
The only thing that affects the amount a projectile will drop is time of flight. If you are shooting downhill or uphill your line of sight is now no longer perpendicular to gravity and a component of your “drop” is now parallel to your line of sight. Wind drift is determined by the difference between time of flight in a vacuum and actual time of flight. This is why BC is king when it comes to wind drift, a high BC will shrink that difference.
