Too much FOC

[Tallg]

First thing to do is establish that an object with higher density of mass will drop fast than an object of lighter density. Since I don't have a bowling ball and a feather handy, I use and ink pen and a piece of paper. Dropped at the same time the pen will hit the floor sooner than the paper. With that we now know the heavy end of the arrow will drop faster than the light end. Drop an arrow from a flat position and the heavy end will hit the ground before the light end. It will be hard to see the difference with the eye, but a half inch is a lot when it comes to flight of a broadhead. The half inch is what I estimated it was when I drop tested my arrow. When in flight, momentum wants to keep the arrow going in a straight line, while gravity is pulling it down. With the point end now slightly lower than the tail due to gravity, both the broadhead and the fletching are catching air and driving the arrow down faster than gravity alone. To test this stick your hand out the window of a car traveling at highway speed. When your hand and arm are flat with the direction of travel, it takes very little effort to hold it straight. All you have to do, is overcome the force of gravity pulling on your arm down. Now point your hand and arm down to see how much force the air applies to your arm. The force of the air can be significantly greater than the force of gravity. This has been a great conversation to have with everyone . I hope it gets people thinking and maybe a qualified engineer of aerodynamics will chime in and help.

 

[Beendare]

I believe an arrow of the same weight with less foc would have the same point of impact.

If high foc helps a mediocre longbow shooter bring down buffalo, doesnt that lend credibility to the high foc argument?

First sentence is true- its a law in physics…then why is your guru trying to fool folks into thinking otherwise?

If you have ever built a high foc arrow, you realize that you end up with a heavy arrow. Was it the arrow weight or FOC that improves penetration? We know its arrow weight….the FOC part has never been proven.

Hypothetical; what do you think the margin of error is for a mediocre- at best- longbow shooter? Its probably as much as 10%….but who knows…there was never a control for that factor ( like a Hooter Shooter)

Now consider that much of the high FOC claims are a low single digit advantage. Thats well within the margin of error of a poor longbow guy. Plus, no legit scientific study has ever come out proving it. The experts ( like Easton engineers) recommend 8-16%.

Myth busted.…and many might be too young to remember but Ashby himself has backed away from his initial “30% + foc threshold” that he claimed had incredible penetration.

Plenty of legit sources out there to get good info from…..vs a guy that uses rubber bands.

 

[MattB]

Now that I think about it more…..

You should have stopped just short of that point.

 

[MattB]

You are misattributing the affect of drag on the piece of paper and fletched arrow to mass. You would need a vacuum chamber to eliminate air resistance to isolate for mass.

Cut the fletchings off an arrow and drop it parallel to the ground. You will be amazed that the even lighter tail end falls faster without the fletchings. Again, not because of the affect of gravity on mass but because of the reduced drag.

 

[Tallg]

You are misattributing the affect of drag on the piece of paper and fletched arrow to mass. You would need a vacuum chamber to eliminate air resistance to isolate for mass.

Cut the fletchings off an arrow and drop it parallel to the ground. You will be amazed that the even lighter tail end falls faster without the fletchings. Again, not because of the affect of gravity on mass but because of the reduced drag.

Both valid points. Hunting in a vacuum you would not get any plane effect on the broadhead or the fletching. Fletching would be worthless in this condition. Not real world conditions though.

Second point is also spot on. Less drag but also denser mass on the knock end. Heaviest end still drops faster.

 

[Wrench]

Pretty easy to settle....drop a high foc and standard arrow from a level position. If the weighted end lands first....you have begun to validate your point.

Other contributing factors like paradox play into the foc game but don't get enough attention.

A broom stick and a garden hose dropped straight down....which one will do the better job of energy transfer to the point of impact?

 

[nettereo16]

Think of an airplane flying nose down but trying to fly horizontal to the ground. A plane has to turn nose up changing its wing plane to an upward position in order for it to go up.

Arrows don’t have lift, unless you have a poorly tuned broadhead

 

[Zac]

I think that all arrows end up flying nock high due to lift created by vanes. Not necessarily lifting up in the air, but rather lifting the vanes higher than the point.

 

[Wrench]

It's hard for an arrow to come off the bow nock low but very easy to do so nock high....the shelf/rest are the limiting factor. The arrow tends to self correct pretty quickly....and from there it's all drag and gravity.

 

[MattB]

Heaviest end still drops faster.

That isn't true and is easily verifiable. I just dropped an unfletched shaft with a field point installed in it 3 times horizontally from shoulder height and it landed horizontally each time - not point first. Just like the laws of gravity suggest it would.

 

[wadegarrett]

First thing to do is establish that an object with higher density of mass will drop fast than an object of lighter density. Since I don't have a bowling ball and a feather handy, I use and ink pen and a piece of paper. Dropped at the same time the pen will hit the floor sooner than the paper. With that we now know the heavy end of the arrow will drop faster than the light end. Drop an arrow from a flat position and the heavy end will hit the ground before the light end. It will be hard to see the difference with the eye, but a half inch is a lot when it comes to flight of a broadhead. The half inch is what I estimated it was when I drop tested my arrow. When in flight, momentum wants to keep the arrow going in a straight line, while gravity is pulling it down. With the point end now slightly lower than the tail due to gravity, both the broadhead and the fletching are catching air and driving the arrow down faster than gravity alone. To test this stick your hand out the window of a car traveling at highway speed. When your hand and arm are flat with the direction of travel, it takes very little effort to hold it straight. All you have to do, is overcome the force of gravity pulling on your arm down. Now point your hand and arm down to see how much force the air applies to your arm. The force of the air can be significantly greater than the force of gravity. This has been a great conversation to have with everyone . I hope it gets people thinking and maybe a qualified engineer of aerodynamics will chime in and help.

----------------
TLDR

Having a heavier FOC does technically affect how quickly the tip "falls", however it's very likely negligible compared to the 100s of other arrow/shooter/zodiac sign/what you had for breakfast/dynamics at play.

If you're starting to see your arrow pitch, you're probably off better doing a bit of tuning of bow/arrows.
----------------

Not an aero engineer, but mechanical is close enough. I'll go step by step and lay out assumptions to simplify things. Let's say we're talking two arrows, A and B, which have identical dimensions, static and dynamic spine reactions -the works. We'll even say they have no fletchings because we're only concerned about differentially-weighted cylinders the only difference between these two arrows is where the balance point is located. Arrow A is heavy FOC, B is not.

As others pointed out, all objects get pulled down by gravity at the same rate. The only thing affecting this rate is the drag (and in lesser effect buoyancy - we'll neglect because we're dealing with air here). If you've poked around physics, you might remember a free body diagram that shows this:

Drag, Fd, is easy to figure out for our two arrows in question since we know the common fixed parameters:

Fd = 0.5 * p * A * Cd *v^2

• density of the air (rho, p-looking thing)
• Effective surface area (A)
• Coefficient of drag (Cd)
• velocity (there's a speed and velocity term, let's assume they're the same - v)

As you can see in there, mass have no effect on drag - it's only real variable is area (which is fixed for us) or speed (which may change for us if the theory that heavier stuff falls faster holds true).

Great, now what about the Fg side? That one is is gravitational force, and it is affected by mass.

F=m*g

• mass of arrow (both arrows are technically the same, but around our centerpoint arrow A is more heavy up front - m. For our purposes this can introduce torque (or pitch))
• gravitational acceleration (g, fixed for all)

So now we pit both those forces against each other and see what happens:

Fnet = Fg - Fd
m * a = m*g - 0.5 * p * A * Cd *v^2
a = g - {0.5 * (1/m)* p * A * Cd *v^2}

This gives us the acceleration (a) of the object based on our parameters. This is the part that's interesting - the mass term is on the bottom, meaning if the mass is greater, technically the acceleration will be greater since the second term (squiggly brackets {} ) will shrink against g. However, if the acceleration is greater then the velocity will also increase - and that one is squared, on top and fighting our mass. That should mean eventually they'll reach a happy medium.... and we're on a freight train to terminal velocity!

While we won't ever reach Vt, it's still interested to plot the battle of mass vs velocity (you need to integrate the acceleration equation to do that, I won't both putting that up but you can look it up). Here is a quick plot of the velocity of an object with respect to time. Imagine we're dropping just the top 6" of a .266" OD arrow in air with a mass of 100 gr for Arrow A (series 1), and 200 gr for Arrow B (series 5) - and every 25gr in between for fun :



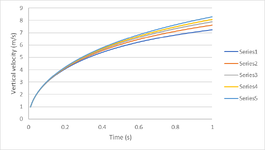
Based on this very quick and very simplified model, we see ~13% difference in the Arrow A tip and Arrow B tip after 1s. But remember - this is not an absolute, it just tells us that there is a bit of torque than can be applied to the arrow over time due to differential weight with a net pitch down. Now this is over 1s of time, and an arrow going 240 FPS (average over range, not restarting the drag calcs) hits a target at 60ft* in 0.25s. According to our rough plot, that's now down to 4% vertical speed difference between arrow A and arrow B. Assuming you're an MOA (archery) shooter at 20yds, 4% of a 2" group is 5/64" difference (at 60yds with 10% difference it's ~39/64", thanks @Blockcaver ) - and that's assuming the velocity differential we're plotting translates effectively to arrow torque...

Hopefully that helps, I know it's easy to get sucked down the vortex.

 

[HighUintas]

Let's say there's 2 arrows. One has a high FOC, the other is perfectly balanced at center.

Drop both arrows at the same time, parallel to the ground. Which one do you think will flip to vertical faster?

 

[sndmn11]

So, if one creates a high BOC arrow then will they see if lift and have a flatter trajectory?

With the point end now slightly lower than the tail due to gravity, both the broadhead and the fletching are catching air and driving the arrow down faster than gravity alone. To test this stick your hand out the window of a car traveling at highway speed. When your hand and arm are flat with the direction of travel, it takes very little effort to hold it straight. All you have to do, is overcome the force of gravity pulling on your arm down. Now point your hand and arm down to see how much force the air applies to your arm. The force of the air can be significantly greater than the force of gravity.

 

[TaperPin]

What's interesting is that the entire point of the argument would be difficult to prove. Im no professional, but I know enough to say that when you change one thing like front weight or TAW, it can change its impact in any number of directions.

I understand the OPS point, but I do not agree.

I have found that when people put really heavy front weight on an arrow, it does really wacky things to how the arrow reacts to being shot, subsequently affecting downrange performance.

Sent from my SM-S918U using Tapatalk

What if someone added a little weight to the rear interior of the arrow before the nock is installed and combined that with a light fieldpoint to equal the heavy broadhead. I‘m not bow hunting anymore, but it would be interesting to validate what everyone thinks is correct.

 

[MattB]

Let's say there's 2 arrows. One has a high FOC, the other is perfectly balanced at center.

Drop both arrows at the same time, parallel to the ground. Which one do you think will flip to vertical faster?

The one with more fletching surface area exposed to the direction of travel due to drag.

 

[Beendare]

This is pretty good from guys that have had the most cutting edge science available to them on FOC- Olympic archers- the one gold medalist Jay Barrs is a bowhunter.

Its funny what they say about guys getting all wrapped up about high FOC.

 

[HighUintas]

The one with more fletching surface area exposed to the direction of travel due to drag.

The surface area of fletchings in relation to directions of travel is same. They are identical in every way except for FOC.

How gh FOC arrow would flip vertical first, I think.

 

[stanginthe11s]

there is so much that goes into this. gravity is constant, but acceleration is not. high FOC arrows fall nose first because a heavier object accelerates faster in relation to gravity. is it enough to matter? not usually. can a BOC arrow fly nock down? yes. when you change center of gravity, many things can happen. in the world of bowhunting, it really isn't enough to matter.

 

[sndmn11]

9.8 meters per second squared

 

[cornfedkiller]

I thought this video was pretty interesting and seemed to make sense, but I'm curious what other's opinions are on the info...